Arithmetic vs Logarithmic Returns - What Investors Need to Know

The article explains the difference between arithmetic and logarithmic returns, and why it’s important for investors to understand the distinction. Arithmetic returns are simple to calculate but can be misleading when it comes to understanding the impact of compounding returns. Logarithmic returns, on the other hand, provide a more accurate picture of the actual returns on an investment by taking into account the effect of compounding. The article concludes that understanding the difference between these two methods is essential for making informed investment decisions and achieving better long-term investment outcomes.

Arithmetic and logarithmic returns are two ways of measuring the change in an investment’s value over a period of time.

Arithmetic returns

Arithmetic returns, also known as simple returns, are calculated by taking the difference between the ending value of the investment and the beginning value, and then dividing by the beginning value. The formula is:

$$ArithmeticReturn = \dfrac{ClosePrice - OpenPrice}{OpenPrice}$$

For example, To calculate the arithmetic return for Apple stock, you’ll need the beginning and ending stock prices for a specific period. Let’s say you want to calculate the arithmetic return for Apple stock for the month of January 2023. Here are the hypothetical stock prices:

• Beginning stock price on January 1, 2023: $150
• Ending stock price on January 31, 2023: $165

Now, we can calculate the arithmetic return using the formula mentioned earlier:

$$ArithmeticReturn = \dfrac{\$165 - \$150}{\$150}$$

The arithmetic return for Apple stock in January 2023 is 0.10, or 10%. This means that the stock’s value increased by 10% during that month.

Logarithmic returns

Log returns, also known as continuously compounded returns, are calculated by taking the natural logarithm of the ratio of the ending value to the beginning value. The formula is:

$$LogReturn = ln(\dfrac{ClosePrice}{OpenPrice})$$

Log returns have a few advantages over arithmetic returns. They are additive across time, meaning that the log return of multiple non-overlapping periods can be found by summing the log returns of each period. This property makes log returns particularly useful for analyzing returns over multiple periods or when calculating portfolio returns. Log returns also exhibit better statistical properties, such as being approximately normally distributed in many cases.

For example, to calculate the log return for Apple stock, you’ll need the beginning and ending stock prices for a specific period. Let’s use the same example as before, calculating the log return for Apple stock for the month of January 2023 with these hypothetical stock prices:

• Beginning stock price on January 1, 2023: $150
• Ending stock price on January 31, 2023: $165

Now, we can calculate the log return using the formula mentioned earlier:

$$LogReturn = ln(\dfrac{\$165}{\$150})$$ $$LogReturn = ln(1.10)$$ $$LogReturn \approx 0.0953$$

The log return for Apple stock in January 2023 is approximately 0.0953, or 9.53%. This means that the stock’s value increased by about 9.53% during that month, when accounting for the compounding effect.

It’s important to note that while the log return and arithmetic return values are close, they are not identical. The log return is more appropriate for multi-period analysis or when considering compounding effects, while the arithmetic return is easier to understand and suitable for single-period calculations.

Additive properties of Logarithmic returns

The additive property of log returns allows you to calculate the overall return of an investment over multiple non-overlapping periods by simply summing the log returns of each period. Let’s use Apple stock as an example with hypothetical data for three consecutive months:

Date	Price
January 1, 2023	$150
February 1, 2023	$165
March 1, 2023	$180
April 1, 2023	$190

First, we’ll calculate the log returns for each month:

$$January 2023 = ln(\dfrac{\$165}{\$150}) \approx 0.0953$$ $$February 2023 = ln(\dfrac{\$180}{\$165}) \approx 0.0870$$ $$March 2023 = ln(\dfrac{\$190}{\$180}) \approx 0.0531$$

Now, we can use the additive property of log returns to calculate the overall return for the three-month period:

$$Total Log Return = 0.0953 + 0.0870 + 0.0531 \approx 0.2354$$

The additive property of log returns simplifies the calculation of returns over multiple periods, making it particularly useful for financial analysis and portfolio management.

The Relationship Between Arithmetic and Log Returns

The chart below exposes the relationship between arithmetic returns and log returns.

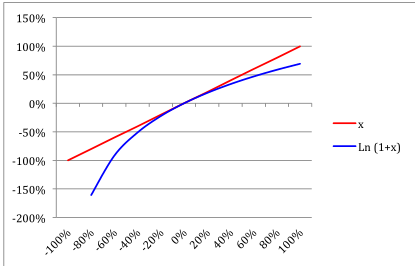
There is no one-to-one relationship between log returns and arithmetic ones; nevertheless you can note that the smaller the return, the more arithmetic and log returns tend to be similar.

Conclusion

In conclusion, understanding the difference between arithmetic and logarithmic returns is essential for any investor who wants to make informed decisions about their portfolio. While arithmetic returns are simple to calculate and provide a clear picture of the average return over a given time period, they can be misleading when it comes to understanding the impact of compounding returns.

On the other hand, logarithmic returns provide a more accurate picture of the actual returns on an investment, by taking into account the impact of compounding. By using logarithmic returns, investors can make better-informed decisions about their investment strategies, and avoid being misled by simple arithmetic calculations.

Ultimately, whether you use arithmetic or logarithmic returns will depend on your investment goals and the specifics of your investment portfolio, but having a clear understanding of the differences between these two methods can help you achieve better long-term investment outcomes.